The Extraordinary Success of General Relativity

This month, people around the world are celebrating the hundredth anniversary of Albert Einstein’s Theory of General Relativity (GR). Although this theory can seem esoteric, it has an important practical application: the accuracy of Global Positioning System (GPS) relies on corrections from GR.

The GPS satellites orbit about 20,000 km (12,000 miles) above the Earth and experience gravity that is four times weaker than found on Earth’s surface. GR tells us that clocks traveling in this weaker field tick more rapidly, at a rate of about 40 thousandths of a second per day. This may not sound like much, but if these differences were left uncorrected they would cause navigational errors to accumulate faster than 10 km (6 miles) per day, as physicist Clifford Will explains in this article about GPS and relativity. By using GPS to successfully navigate around unfamiliar roads, people are inadvertently testing and retesting the accuracy of GR.

In astrophysics, GR has been tested and applied in multiple ways, including many that involve Chandra observations. Several years ago scientists used Chandra to test GR over distances that are much greater than those of Earth-orbiting satellites. They showed that GR correctly predicts the rate of growth of galaxy clusters and that GR performs better than an alternative model of gravity. They have also provided a new way to study the accelerating expansion of the Universe.

Figure 1: Known officially as Abell 2744, this system has been dubbed “Pandora’s Cluster” because of the wide variety of different structures found. Data from Chandra (red) show gas with temperatures of millions of degrees. In blue is a map showing the total mass concentration (mostly dark matter) based on data from the Hubble Space Telescope, the Very Large Telescope (VLT), and the Subaru telescope. Optical data from HST and VLT also show the constituent galaxies of the clusters. Astronomers think at least four galaxy clusters coming from a variety of directions are involved with this collision.

In a kind of cosmic GPS, GR has had a profound effect on our ability to map the location of matter in the Universe. In particular, gravitational lensing – the bending of light caused by massive objects curving space – has allowed astronomers to “see” the invisible by making maps of dark matter. The best-known example of this work is the Bullet Cluster, but other galaxy clusters have been studied using similar techniques, including MACS J0025.4-1222, Abell 520 and Abell 2744 (see Figure 1). A critical feature of these results was combining X-ray data from Chandra with optical data from observatories like the Hubble Space Telescope, to see separations between normal, visible matter and dark matter.

Gravitational lenses can also sometimes act as magnifying glasses, increasing the light from distant objects so they can be studied in much greater detail than would be possible without the lens. This was the case with the direct measurement of a black hole’s spin in the quasar RX J1131-1231.

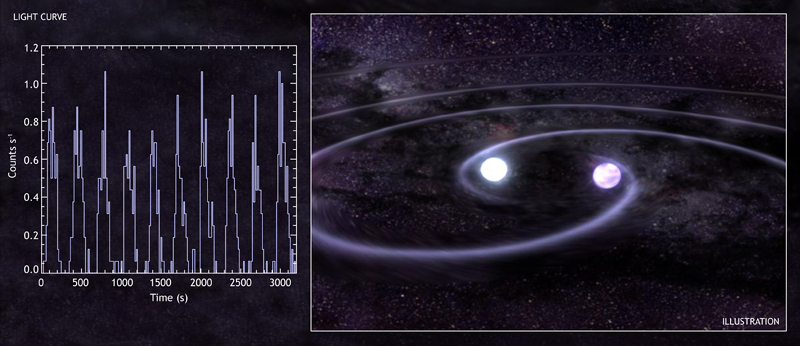
Figure 2: Chandra data (above, graph) from observations of RX J0806.3+1527 (or J0806), show that its X-ray intensity varies with a period of 321.5 seconds. This implies that J0806 is a binary star system where two white dwarf stars are orbiting each other (above, illustration) approximately every 5 minutes. The short orbital period implies that the stars are only about 50,000 miles apart, a fifth of the distance from the Earth to the Moon, and are moving in excess of a million miles per hour. According to GR, such a system should produce gravitational waves - ripples in space-time - that carry energy away from the system at the speed of light. Energy loss by gravitational waves will cause the stars to move closer together. X-ray and optical observations indicate that the orbital period of this system is decreasing by 1.2 milliseconds every year, which means that the stars are moving closer together at a rate of about 2 feet per day.

Another prediction of GR is that certain objects, such as close pairs of white dwarfs, neutron stars or black holes, should produce gravitational waves. These are ripples in spacetime that travel outward at the speed of light. The shrinking separation of double stars has been explained by energy lost with the emission of gravitational waves. On much larger scales, astronomers have found evidence for a supermassive black hole that is being ejected from its host galaxy. The black hole may have collided and merged with another black hole and then received a powerful recoil kick from gravitational waves. If this mechanism is indeed the correct explanation, then as theorist Avi Loeb explained in a blog post for us, this black hole provided the "first observational validation of Einstein's equations in the unexplored regime of dynamical strong gravity, which is responsible for gravitational wave kicks.”

The direct detection of gravitational waves would be one of the biggest advances in astrophysics in decades, and strenuous efforts to achieve this are ongoing. One major project, called Advanced LIGO, is US-based and in the next few years may start making detections of gravitational waves from dramatic events like mergers between two neutron stars. Several other projects are using pulsars to search for gravitational waves from much slower events, such as orbiting pairs of supermassive black holes. These projects include the North American Nanohertz Observatory for Gravitational Waves (NANOGrav) and the Parkes Pulsar Timing Array.

One of the most spectacular applications of Einstein’s theory is the use of GR to describe the behavior of matter near the event horizon of a black hole. For example, the spin rate of matter rotating around a black hole, and the spin rate of the black hole itself can be estimated using GR and X-ray observations, as with the result for RX J1131-1231 mentioned earlier. This result, therefore, is notable for involving two major applications of GR, the strong gravity around a black hole and gravitational lensing.

Despite the incredible successes of GR, no theory is complete. Ultimately, black holes represent a key shortcoming of GR, as this theory breaks down at the very center of a black hole, in a tiny region of extraordinarily high density called a singularity. There needs to be a melding of GR with another extremely successful theory – quantum mechanics – to treat black hole singularities. As this challenging work continues, we expect that GR will continue, for some time, to be our best theory for mapping the Universe.

By Peter Edmonds