Purpose: To determine if two end products of stellar evolution – GK Per and Cen X-3 – could be white dwarfs or neutron stars by calculating the periods of X-ray pulses emitted by the two stellar cores using data recorded by the Chandra X-ray Observatory.
Background:
SS Cygni Light Curve, AAVSO
Variable Stars are stars that vary in magnitude (brightness). The behavior of stars that vary in magnitude can be studied by measuring their changes in magnitude over time and plotting the changes on a graph called a light curve. The example to the left is a light curve that shows the variability of SS Cygni over a 300 day period of observation. SS Cygni is a cataclysmic variable – stars that have occasional violent outbursts caused by thermonuclear processes either in their surface layers or deep within their interiors.
Illustration by David T Hardy, Artist
SS Cygni is also an example of a subclass of cataclysmic variables called dwarf novae. This is a close binary system consisting of a red dwarf star, cooler and less massive than the Sun, a white dwarf, and an accretion disk surrounding the white dwarf. The brightening of this system occurs when instability within the disk forces some of the disk material to drain down to the surface of the white dwarf triggering a Illustration by David T Hardy, Artist thermonuclear explosion. The SS Cygni light curve above shows 5 thermonuclear events within the 300 day observation period.
The SS Cygni light curve above was observed in the optical part of the spectrum and displays the dynamics among the accretion disk - the material in the disk that was accreted from its companion star - and the surface of the white dwarf. The white dwarf itself is the stellar core of a Sun-sized star at the end of its evolutionary history – a rotating carbon core. The light curve above is produced by the dynamics of the system and not the white dwarf itself, which emits most of its radiation in X-rays.
SNR G292.0+1.8, Chandra
More massive stars, which catastrophically collapse during supernova events, produce different types of stellar cores – including neutron stars – within the supernova remnants (SNR). Rotating neutron stars are called pulsars. Both white dwarfs and neutron stars are stellar cores – end products that remain after the evolution of their progenitor stars. Both objects rotate, though the smaller and denser neutron stars rotate much more rapidly than the larger and less dense white dwarfs. White dwarfs cannot exceed 1.4 solar masses, and neutron stars 2.4 solar SNR G292.0+1.8, Chandra masses. Neutron stars can also have companion stars and accrete materials from the companion star into an accretion disk surrounding the neutron star; a similar configuration to the SS Cygni star system described above.
Both white dwarfs and neutron stars generate strong emissions in X-rays, and the changes in X-ray brightness over time can be observed and recorded. The resulting light curve, just like the optical light curve of SS Cygni, can be used to determine the properties of these stellar cores.
Illustration of an X-ray Binary
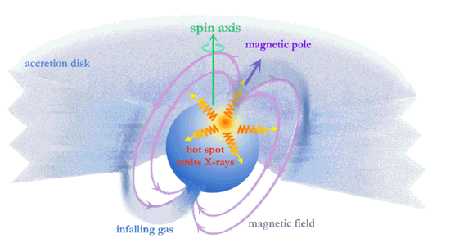
Some stellar cores emit X-rays that exhibit some regularity, so it is suspected that some sort of dynamic mechanism is producing the X-ray pulses that manifest themselves as changes in X-ray brightness. One such mechanism for rotating objects is “hot spots” which rotate into and out of the line of sight of the Chandra X-ray Observatory.
Illustration of an Accretion Powered Pulsar
A "hot spot" on a white dwarf can occur if a white dwarf with a magnetic field accretes matter from the companion star, and the accretion disk is disrupted at small radii by the white’s dwarf's magnetosphere. Material would then travel along the magnetic field lines. Above the surface of the white dwarf, the freefall kinetic energy of the material is converted into thermal energy, producing a strong shock wave. The material settles onto the surface of the white dwarf near the magnetic poles where it cools and emits X-rays. If the magnetic axis is offset from the spin axis, the X-ray emission will pulse with the spin period of the white dwarf. A neutron star in a binary system can become an accretion powered pulsar – producing a pulsing X-ray emission the same way as described for the white dwarf and shown in the illustration above.
GK Per and Cen X-3 are stellar cores that have been imaged by Chandra. Both objects exhibit variations in X-ray brightness that appear to display some regularity. This activity uses ds9 – an image analysis software package – to analyze GK Per and Cen X-3 – in order to determine if they are white dwarfs and/or neutron stars. The physics equations and numbers necessary for the calculations are provided. It is necessary to download the ds9 toolbox in order to remotely access the dedicated Linux servers which process the analysis commands.
Procedure:
1. Download & Install ds9 (http://chandra-ed.harvard.edu/install_2014.html)
2.Open ds9. Go to Analysis>Virtual Observatory>Chandra-Ed Archive Server and click Obs ID 3454 - CHANDRA HETG SPECTROSCOPY OF GK PER IN OUTBURST on the screen that comes up. (Do not close this window – another image will be loaded into the window later.)
3.Regions have been pre-drawn. User serveral different Scales and Colors to see how the details of GK Per change. Go to Analysis>Chandra Ed Analysis Tools>FTOOLS Light Curve and click OK. On the light curve generated, zoom in on an area on the graph by either left clicking and dragging a box around a region of the graph or by changing the x-axis range under Graph>Range until you can determine if there appears to be a periodic x-ray pulse.
4.Go to Analysis>Chandra Ed Analysis Tools>FTOOLS Power Spectrum and click OK. This command does a fast Fourier Transform on the data to search for periodicities. If the data is not periodic, one large peak will not appear as it will for GK Per. Zoom in on the peak until its frequency can be determined. Convert the frequency to period (period = 1/frequency).
5.Go to Analysis>Chandra Ed Analysis Tools>FTOOLS Period Fold. This will help to check the accuracy of the period found in step 4. Enter the value for this period in the window that comes up and click OK. To understand what this command is doing, picture a drawing of a sine wave on a long piece of paper. Cut this paper into sections, each section (one cycle) one period long, and put each cycle on top of the first one, adding all the sine wave sections together. If the cuts are all not exactly one period, then when the sine waves are added parts of the waves cancel out and the composite wave will have a smaller amplitude. How does the Period Fold graph look? Try it again with a period several seconds different than the one used before. Which graph is more sine-like and has the highest amplitude? If necessary, try Period Fold again with different periods until the best graph is produced. Record this period. This is equal to GK Per’s spin period as discussed in the background information.
6.Go to "chandra-ed.cfa.harvard.edu" window and hit the back arrow. Click Obs ID 1943 – THE WIND AND ACCRETION DISK IN CEN X-3/V779 CEN. Make a light curve, power spectrum, and period fold for this data to find the period of Cen X-3.
Calculations and Interpretations:
The acceleration due to gravity (g) on the surface of a star (according to Newton's Universal Law of Gravitation) is given by
g = (GM)/R2 where G = 6.67 X 10-11 Nm2/kg2, M=star's mass and R = star's radius
Centripetal acceleration (ac) of an object on the surface of a star at its equator is given by
ac = V2/R and since V = 2πR/T for an object moving in a circle
ac = 4π2R/T2, where R = star’s radius and T = star’s spin period
If the centripetal acceleration on material on the star’s surface for a given period is less than the acceleration due to gravity, the gravitational force would be enough to hold the material on the surface and the star could sustain such a period without disruption.
1. Find the acceleration due to gravity on the surface of a white dwarf. Let the mass of a white dwarf be approximately one solar mass or 2.0 X 1030 kg and its radius, approximately that of Earth or 6.4 X 106 m.
2. Find the acceleration due to gravity on the surface of a neutron star. Let the mass of a neutron star be two solar masses or 4 X 1030 kg and its radius be 10.0 km.
3. Assume GK Per is a white dwarf. Calculate the centripetal acceleration of material on the surface of GK Per (using the period you found from the power spectrum). According to the calculations, can GK Per be a white dwarf*? Why or why not?
4. If the answer above is “no”, repeat #3 assuming GK Per is a neutron star.
5. Repeat #3 and #4 for Cen X-3. Is it more likely that Cen X-3 is a white dwarf or a neutron star? Why?
*Note: If it is possible that a star is a white dwarf according to the types of calculations performed in this activity, other analysis would be necessary to determine if an object is actually a white dwarf, such as examination of its temperature and luminosity.
Revised: July 08, 2014