Purpose: To use the observed size of the Cassiopeia A supernova remnant (SNR) from its X-ray image and an estimated rate of expansion to calculate its approximate age.
Background:
There is controversial evidence that the British astronomer John Flamsteed observed and recorded the Cas A supernova event in his journal on the evening of August 16th, 1680. He observed a star that was near the position of Cas A, not observed by anyone else, and was never seen again - it could have been the explosion that produced Cas A.
Historia Coelestis, 1725
NOTE: You do not need to use the ds9 image analysis software for this activity. Screen shots of the necessary data and images from ds9 are provided, and all necessary equations and conversion factors are listed at the end of the activity.
Procedure:
How Big is Cas A?
1.Record the radius of Cas A in pixels given in the "Circle" information box on the ds9 screenshot shown in Figure 1. Note that the jet in the upper left has been excluded from the region surrounding Cas A – the dynamics of this jet formation are different that those of the overall expansion of the SNR. Record the x- and y-coordinates of the center of the region to use in #8 below.
2.To find the radius of Cas A in meters, use the small angle approximation. Imagine the lines of sight from Cas A to Earth. These lines form an angle, Θ. On a Chandra image, 1 pixel corresponds to 0.5 arc seconds of angle. Find the angular size of the radius of Cas A in arc seconds and convert to radians.
3.The lines of sight are the radii of an imaginary circle with Earth at the center and Cas A on the circumference. The radius of this circle is the distance to Cas A. For very small angles, the radius of Cas A is approximately equal to the arc length transcribed by these lines of sight. Therefore, the small angle formula is as follows, where Θ is in radians:
Θ= (radius of Cas A) / (distance to Cas A)
Using the small angle formula and a distance to Cas A of ~11,100 light years, find the radius of Cas A in meters.
What is the rate of expansion of Cas A?
The average amount of energy released in a supernova explosion is ~1044 Joules, and approximately one quarter of the energy drives the expansion of the remnant. Although the initial collapse and rebound of the core ejects the outer layers of the star, most of the gas in the remnant is not from the star. As the ejected material expands outwards, it encounters and intermingles with the interstellar medium (ISM) and propels it outward, building up the outer shock wave. The volume through which the remnant has expanded and the density of the ISM determine the amount of material in the shell. On average this density is approximately 10-21 kg/m3.
4.The Cas A SNR is basically a sphere. Determine the mass of the gas within the remnant using the radius previously calculated in #1.
5.Calculate the velocity of the gas (the expansion velocity of Cas A).
6.Use the expansion velocity and the radius of Cas A to estimate its age. Convert from seconds to years.
What is the displacement of the core remnant from the center of the SNR?
7.A dot located in the center of the remnant is the remaining core of the collapsed star. Use figure 2 to find the physical x- and y-coordinates of the core.
8.Use the coordinates of the center of the region (from #1 above) to find the displacement of the stellar core from the center.
9.Find the average velocity of the stellar core for this displacement.
10.Using this average velocity, find its kinetic energy. Evidence indicates the core is a neutron star with a typical mass of about 1.4 solar masses.
Conclusions and Analysis:
1. How does your estimated age for Cas A compare to 330 years? Does it have the same order of magnitude?
2. What approximations and assumptions were made in this method of estimating the age of a supernova remnant? How might these affect the results?
3. Could Cas A be the supernova observed by John Flamsteed in 1680? Why or why not?
Extensions:
Research other methods of determining the ages of supernova remnants and describe your findings.
Resources:
The Three-dimensional Structure of the Cassiopeia A Supernova Remnant
http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1995ApJ...440..706R
The "Guest Star" of 386AD
http://physicsphunhouse.com/chandra_activities/Supernova_G11_Activity.doc
Chandra X-Ray Observations of G11.2-0.3: Implications for Pulsar Ages
http://www.iop.org/EJ/abstract/0004-637X/560/1/371
Finding the Age of Supernova Remnant N157B
http://imagine.gsfc.nasa.gov/docs/features/news/25feb98b.html
Survivor Found From Tycho's Supernova
http://www.universetoday.com/am/publish/tycho_supernova_survivor.html
A VLA Study of the Expansion of Tycho's Supernova Remnant
http://www.iop.org/EJ/abstract/0004-637X/491/2/816/
Ice Core Records – From Volcanoes to Supernovas
http://chandra.harvard.edu/edu/formal/index.html
Figure 1. Finding the radius of Cas A
Figure 2. Locating the core remnant (physical coordinates)
Equations and Conversion Factors
Conversion Factors/constants:
60 arc sec = 1 arc min
60 arc min = 1 deg
360 deg = 2π rad
1 light year = 9.46 x 1015 meters
mass of the sun = 2.0 x 1030 kg
Small Angle Formula:
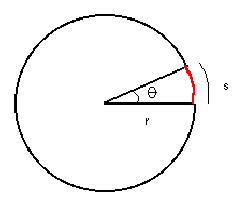
angle in radians (Θ) = [arc length (s)] / [radius (r)]
therefore, for astronomical objects with small angular sizes:
angular size as viewed from Earth (Θ) = (actual size of object) / (distance to object)
Additional Equations:
density = mass/volume
volume of a sphere = 4/3 π r3
kinetic energy = ½ (mass)(velocity)2
velocity = distance/time
distance between 2 points = sqrt [ (x2 - x1)2 + (y2 - y1)2 ]




